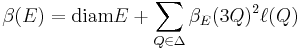Analyst's traveling salesman theorem
The Analyst's Traveling Salesman Problem is an analog of the traveling salesman problem in combinatorial optimization. In its simplest and original form, it asks under what conditions may a set E in two-dimensional Euclidean space  be contained inside a rectifiable curve of finite length. So while in the original traveling salesman problem, one asks for the shortest way to visit every vertex in a graph with a discrete path, this analytical version requires the curve to visit perhaps infinitely many points.
be contained inside a rectifiable curve of finite length. So while in the original traveling salesman problem, one asks for the shortest way to visit every vertex in a graph with a discrete path, this analytical version requires the curve to visit perhaps infinitely many points.
Contents |
β-numbers
A posteriori, for E to be contained in a rectifiable curve Γ, since Γ has tangents at H1-almost every point in Γ (where H1 denotes one-dimensional hausdorff measure), E must look flat when you zoom in on points in E. This suggests that a condition that would tell us whether a set could be contained in a curve must somehow incorporate information about how flat E is when we zoom in on points of E at different scales.
This discussion motivates the definition of the following quantity:
Where Q is any square, 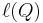 is the sidelength of Q, and dist(x, L) measures the distance from x to the line L. Intuitively,
is the sidelength of Q, and dist(x, L) measures the distance from x to the line L. Intuitively, 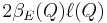 is the width of the smallest rectangle containing the portion of E inside Q, and hence
is the width of the smallest rectangle containing the portion of E inside Q, and hence 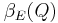 gives us a scale invariant notion of flatness.
gives us a scale invariant notion of flatness.
Jones' traveling salesman theorem in R2
Let Δ denote the collection of dyadic squares, that is,
where 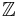 denotes the set of integers. For a set
denotes the set of integers. For a set 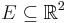 , define
, define
where diam E is the diameter of E. Then Peter Jones'[1] Analyst's Traveling Salesman Theorem may be stated as follows:
- There is a number C > 0 such that whenever E is a set with such that β(E) < ∞, E can be contained in a curve with length no more than Cβ(E).
- Conversely (and substantially more difficult to prove), if Γ is a rectifiable curve, then β(Γ) < CH1(Γ).
Generalizations and Menger curvature
Euclidean space and Hilbert space
- The Traveling Salesman Theorem was shown to hold in general Euclidean spaces by Kate Okikiolu,[2] that is, the same theorem above holds for sets
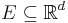 , d > 1, where Δ is now the collection of dyadic cubes in
, d > 1, where Δ is now the collection of dyadic cubes in 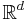 defined in a similar way as dyadic squares. In her proof, the constant C grows exponentially with the dimension d.
defined in a similar way as dyadic squares. In her proof, the constant C grows exponentially with the dimension d.
- With some slight modifications to the definition of β(E), Raanan Schul[3] showed Traveling Salesman Theorem also holds for sets E that lie in any Hilbert Space, and in particular, implies the theorems of Jones and Okikiolu, where now the constant C is independent of dimension. (In particular, this involves using β-numbers of balls instead of cubes).
Menger curvature and metric spaces
- Hahlomaa[4] further adjusted the definition of β(E) to get a condition for when a set E of an arbitrary metric space may be contained in the Lipschitz-image of a subset
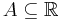 of positive measure. For this, he had to redefine the definition of the β-numbers using menger curvature (since in a metric space there isn't necessarily a notion of a cube or a straight line).
of positive measure. For this, he had to redefine the definition of the β-numbers using menger curvature (since in a metric space there isn't necessarily a notion of a cube or a straight line).
- Menger curvature, as in the previous example, can be used to give numerical estimates that determine whether a set contains a rectifiable subset, and the proofs of these results frequently depend on β-numbers.
References
- ^ Jones, Peter (1990). "Rectifiable sets and the Traveling Salesman Problem". Inventiones Mathematicae 102: 1–15. doi:10.1007/BF01233418.
- ^ Okikiolu, Kate (1992). "Characterization of subsets of rectifiable curves in Rn". J. of the London Math. Soc. 46: 336–348.
- ^ Schul, Raanan (2007). "Subsets of Rectifiable curves in Hilbert Space—The Analyst's TSP". J. d'Anal. Math. 103: 331–375.
- ^ Hahlomaa, Immo (2005). "Menger curvature and Lipschitz parametrizations in metric spaces". Fund. Math. 185: 143–169.
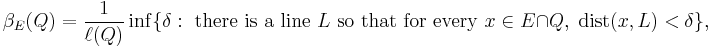
![\Delta=\{[i2^{k},(i%2B1)2^{k}]\times[j2^{k},(j%2B1)2^{k}]: i,j,k\in\mathbb{Z}\},](/2012-wikipedia_en_all_nopic_01_2012/I/8b4212459fef78c46869a0d4866b61d3.png)